Kann die Zahnzahl eines Getriebes weniger als 17 sein?

Zahnräder sind ein im Alltag weit verbreiteter Bauteiltyp, sei es in der Luftfahrt, Frachtschiffen, Automobilen und so weiter. Bei der Konstruktion und Verarbeitung von Zahnrädern gibt es jedoch Anforderungen an die Zähnezahl. Manche behaupten, dass Zahnräder mit weniger als 17 Zähnen nicht rotieren können, während andere darauf hinweisen, dass es viele Zahnräder mit weniger als 17 Zähnen gibt, die richtig funktionieren. Tatsächlich sind beide Aussagen korrekt. Wisst Ihr warum?

Warum beträgt die Zähnezahl 17?

Warum gerade 17 und nicht eine andere Zahl? Was die Zahl 17 betrifft, hat dies etwas mit der Herstellmethode der Zähne zu tun. Wie in der folgenden Abbildung gezeigt wird, ist eine weit verbreitete Methode die Verwendung eines Wälzfräser zur Bearbeitung.

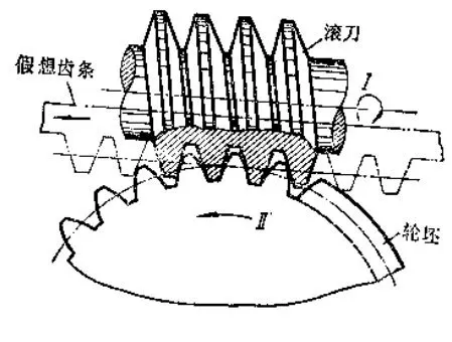
Wenn die Zahnzahl klein ist, tritt ein Phänomen namens Unterfertigung auf, das die Stärke der hergestellten Zahnräder beeinflusst. Was ist Unterfertigung? Sie bedeutet, dass der Fuß geschnitten wird. Beachten Sie das rote Rechteck in der Abbildung:

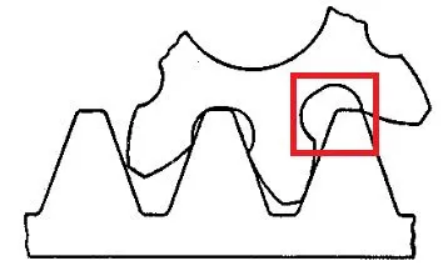
Wenn der Schnittpunkt zwischen dem Zahnspitzenkreis und der Mittellinie den Grenzkontaktpunkt des bearbeiteten Zahnrads überschreitet, wird ein Teil des Evolventenprofils am Fuß des Zahnrads entfernt. Dieses Phänomen wird als Unterfertigung bezeichnet.

In welchen Fällen kann Unterfertigung vermieden werden? Die Antwort liegt in der Zahl 17, die einem Spitzenhöhenkoeffizienten von 1 und einem Druckwinkel von 20 Grad entspricht. Zunächst können Zahnräder rotieren, da die oberen und unteren Zähne eine gute Übertragungsbeziehung bilden müssen. Nur wenn die Verbindung zwischen beiden vorhanden ist, kann ihre Funktion eine stabile Beziehung sein. Am Beispiel von Evolventenzahnrädern: Eine gute Verzahnung zwischen den beiden Rädern ermöglicht es ihnen, ihre Funktion auszuführen. Es gibt zwei Arten: Geradverzahnte Zylinderschnecken und Schrägverzahnte Zylinderschnecken. Das Standard-geradverzahnte Rad hat einen Spitzenhöhenkoeffizienten von 1, einen Fuss-höhenkoeffizienten von 1,25 und einen Druckwinkel von 20 Grad. Beim Zahnradbearbeitung, wenn das Zahnradschiff und das Werkzeug wie zwei Zähne sind. Wenn die Anzahl der Zähne des Schiffs weniger als ein bestimmter Wert ist, wird die Wurzel des Zahnes ausgehöhlt, was Unterfutterung genannt wird. Wenn die Unterfutterung zu klein ist, beeinflusst dies die Stärke und Stabilität des Zahnrads. Die 17, die hier erwähnt wird, bezieht sich auf Zähne. Wenn wir nicht über die Arbeitswirkung des Zahnrads sprechen, spielt es keine Rolle, wie viele Zähne es hat, es funktioniert und kann betrieben werden. Außerdem ist 17 eine Primzahl, was bedeutet, dass die Übereinstimmung eines Zahnes mit einem anderen Zahn in einer bestimmten Anzahl von Umdrehungen minimal ist, und die Kraft wird nicht an derselben Stelle für längere Zeit liegen. Zähne sind Präzisionsinstrumente, obwohl es bei jedem Zahn Fehler geben kann, aber die Wahrscheinlichkeit, dass durch 17 Wellenverschleiß verursacht wird, ist wirklich zu groß, daher kann es sich bei 17 zwar kurzfristig bewegen, aber nicht langfristig. Das Problem tritt jedoch auf! Es gibt immer noch viele Getriebe auf dem Markt mit weniger als 17 Zähnen, und sie funktionieren weiterhin gut, wie Bilder belegen.

Einige Netizens haben jedoch hingewiesen, dass es tatsächlich möglich ist, durch Änderung der Fertigungsmethode normale Evolventengetriebe mit weniger als 17 Zähnen herzustellen. Natürlich können auch solche Räder leicht stecken bleiben (aufgrund von Zahneingriff, kein Bild gefunden, bitte vorstellen), und auf diese Weise kann es sich wirklich nicht bewegen. Es gibt auch viele entsprechende Lösungen, wobei versetzte Räder am häufigsten verwendet werden (alltäglich gesprochen, bedeutet dies, das Werkzeug etwas zu verschieben, wenn man schneidet), und es gibt auch Schrägspalt-Räder, Zykloidenräder usw. Es gibt auch ein universelles Zykloidenrad.

Ein weiterer Netizensichtpunkt: Es scheint, dass alle immer noch zu sehr an Büchern glauben, und ich weiß nicht, wie viele Leute in ihrer Arbeit gründlich Zahnräder studiert haben. Die Herleitung, dass die Zähne eines Zahnrads größer als 17 sein müssen im Maschinenprinzipkurs, um keine Unterfertigung zu verursachen, basiert darauf, dass der Radius R der Vorderflanke des Zahnradschneidwerkzeugs 0 ist. Tatsächlich, wie können Werkzeuge in der industriellen Produktion keinen Radius R haben? (Ohne Radius R sind die Werkzeuge scharf, konzentriert sich die Spannung, es gibt leicht Risse während der Wärmebehandlung und es gibt leicht Verschleiß oder Risse während der Nutzung). Und selbst wenn das Werkzeug keinen Radius R hat, ist die maximale Zahnanzahl, bei der Unterfertigung auftritt, nicht notwendigerweise 17 Zähne, also ist die Aussage, dass 17 Zähne die Bedingung für Unterfertigung sind, tatsächlich diskussionswürdig! Schauen wir uns ein paar Bilder an.

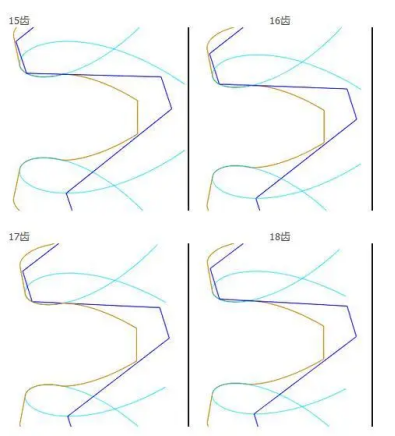
Aus der Abbildung kann man sehen, dass bei Verwendung eines Werkzeugs mit einem R-Winkel von 0 an der vorderen Schneide beim Zähneformen von 15 bis 18 Zähnen keine deutlichen Änderungen an der Übergangskurve am Zahnfuß auftreten. Warum sind dann 17 Zähne die Anzahl, ab der involute gerade Zähne Unterfertigung verursachen?

Ich denke, diese Abbildung, die das Konzept veranschaulicht, sollte den Maschinenbau-Studenten bekannt sein, die einen Zahnradgenerator verwendet haben. Es ist zu sehen, dass die Größe des Werkzeug-R-Winkels die Unterfertigung des Zahnrads beeinflusst.

Die violette erweiterte äußere Epitrochoidenkurve des Zahnfußteils in der Abbildung ist die Zahnprofillinie nach dem Unterfressen des Zahnfußes. Inwieweit beeinflusst das Unterfressen des Zahnfußes die Verwendung eines Zahnrades? Dies wird durch die relative Bewegung der Spitze eines Zahnes des anderen Rades und den Stärkeüberhang des Zahnfußes bestimmt. Wenn die Zahnspitze des verbundenen Rades nicht mit dem unterfressenen Teil in Einklang tritt, können diese beiden Räder normal rotieren (Hinweis: Der unterfressene Teil ist ein nicht-involutiver Zahnbogen. Die Verzahnung eines nicht-involutiven Zahnbogens mit einem involutiven Zahnbogen führt unter nicht speziellen Designbedingungen normalerweise zu einer nicht-konjugierten Verzahnung, das heißt, es kommt zu Interferenzen).

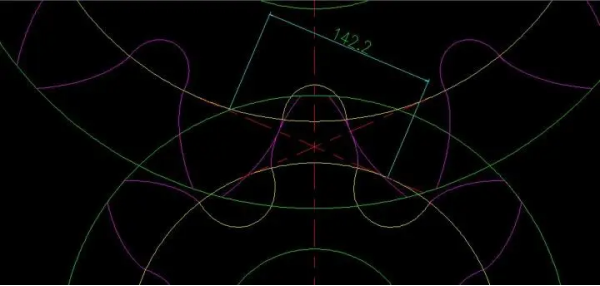
Aus dieser Abbildung kann man sehen, dass die Verzahnungsgerade dieser beiden Räder genau an dem Kreis mit dem maximalen Durchmesser entlang reibt, der der Übergangskurve der beiden Räder entspricht (Anmerkung: Der violette Teil ist das Evolventenradprofils, der gelbe Teil ist der Unterlaufbereich, und die Verzahnungsgerade darf nicht unter den Basiskreis eindringen, da es unterhalb des Basiskreises keine Evolvente gibt. Der Eingriffspunkt der beiden Räder in jeder Position befindet sich auf dieser Geraden), das heißt, diese zwei Räder können gerade normal verziehen. Natürlich ist dies im Ingenieurwesen nicht zulässig, die Länge der Verzahnungsgeraden beträgt 142,2, und dieser Wert ⁄ Basiszahnhöhe = Überlappverhältnis.

Manche Menschen sagen auch: Erstens, die Voraussetzung dieser Frage ist falsch. Eine Zähnezahl von weniger als 17 beeinflusst nicht die Verwendung (die Beschreibung dieses Punkts in der ersten Antwort ist falsch; die drei Bedingungen für ein korrektes Zahnradvergleich sind unabhängig von der Zähnezahl), aber 17 Zähne können unter bestimmten spezifischen Umständen einige Unannehmlichkeiten bei der Bearbeitung verursachen. Hier gibt es mehr Wissen über Zahnräder zu ergänzen.

Erstens sprechen wir über die Evolventenkurve. Die Evolventenkurve ist das am weitesten verbreitete Zahnschaftprofil. Warum also ist es eine Evolventenkurve? Was unterscheidet diese Linie von einer Geraden oder einem Bogen? Wie in der folgenden Abbildung gezeigt, ist es eine halbe Evolventenkurve eines Zahnes.

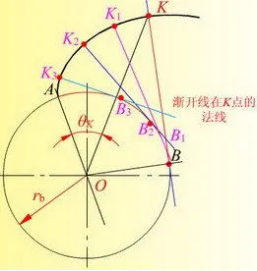
Die Evolventenkurve kann in einem Satz beschrieben werden als die Bahn eines festen Punktes auf einer geraden Linie, wenn diese Linie sich an einem Kreis abrollt. Ihr Vorteil ist offensichtlich. Wenn zwei Evolventenkurven ineinandergreifen, wie in der folgenden Abbildung dargestellt.

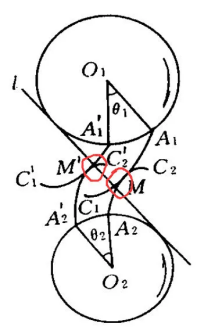
Wenn die beiden Räder rotieren, ist die Richtung der Kraft am Berührungspunkt (z. B. M, M') immer auf derselben Geraden, und diese Gerade steht senkrecht zur Berücksflächene (Schnittfläche) der beiden Evolventenformen. Da sie senkrecht steht, tritt zwischen ihnen keine "Verschiebung" und "Reibung" auf, was objektiv die Reibung während des Zahnrad-Eingriffs verringert, wodurch nicht nur die Effizienz gesteigert wird, sondern auch die Lebensdauer des Zahnrads verlängert wird.

Natürlich ist die Evolvente als der am weitesten verbreitete Zahnpaarprofiltyp nicht unsere einzige Wahl.

Lassen Sie uns noch einmal über "Unterfertigung" sprechen. Als Ingenieure müssen wir nicht nur prüfen, ob es auf theoretischer Ebene machbar ist und ob das Ergebnis gut ist, sondern vor allem müssen wir Wege finden, um die theoretischen Dinge umzusetzen, was Materialauswahl, Fertigung, Genauigkeit, Prüfung und andere Aspekte betrifft.

Die gängigen Bearbeitungsverfahren für Zahnräder werden im Allgemeinen in das Formverfahren und das Erzeugungsverfahren unterteilt. Beim Formverfahren wird die Zahnform direkt mit einem Werkzeug geschnitten, das der Zwischenraumform zwischen den Zähnen entspricht. Dazu gehören im Allgemeinen Fräser, Schmetterlings schleifringe etc.; das Erzeugungsverfahren ist komplexer und kann als das Verknüpfen zweier Zahnräder verstanden werden, wobei ein Zahnrad sehr hart (Werkzeug) ist und das andere sich noch im Rohzustand befindet. Der Vorgang des Verknüpfens erfolgt durch allmähliches Annähern von einem Zustand weiter auseinander bis zum normalen Verknüpfungszustand, währenddessen das neue Zahnrad geschnitten wird. Wenn Sie interessiert sind, können Sie "Maschinenbau-Prinzipien" für eine detaillierte Studie finden.

Die Generierungsmethode wird weit verbreitet eingesetzt, aber wenn das Rad weniger Zähne hat, überschneidet sich die Zahnspitzenlinie des Werkzeugs mit der Verzahnungsstrecke und überschreitet den Grenzpunkt der Verzahnung des zu schneidenden Zahnrads. In diesem Fall wird der Fuß des Zahnrads, das verarbeitet wird, übermäßig entfernt. Da der Teil des Unternehmens die Grenzverzahnung überschreitet, beeinflusst es die normale Verzahnung des Zahnrads nicht, jedoch hat es den Nachteil, dass es die Stärke des Zahnrads schwächt. Solche Zahnräder sind bei Verwendung in schwerbelasteten Anwendungen wie Getrieben anfällig für Zahnbruch, wie in der folgenden Abbildung dargestellt, zeigt ein Modell eines 2-Modul-8-Zähne-Rades, das normal verarbeitet wurde (mit Unternehmenswirkung).

Und 17 ist die Grenzzahl der Zähne, die unter dem Getriebe-Standard in unserem Land berechnet wurde. Getriebe mit weniger als 17 Zähnen werden ein „Unterschnitt-Phänomen“ aufweisen, wenn sie normal mit der Generationsmethode verarbeitet werden, und zu diesem Zeitpunkt muss die Bearbeitungsmethode angepasst werden, wie zum Beispiel durch Verschiebung, wie in der folgenden Abbildung gezeigt: Es handelt sich um ein Getriebe mit Modul 2 und 8 Zähnen, das durch Verschiebung verarbeitet wurde (kleiner Unterschnitt).

Natürlich ist der hier beschriebene Inhalt nicht umfassend, und es gibt noch viele weitere interessante Aspekte in der Mechanik. Auch gibt es bei der Fertigung dieser Teile im Ingenieurwesen noch mehr Probleme. Diejenigen, die sich für Goldpulver interessieren, könnten sich vielleicht stärker damit beschäftigen.

Fazit: Die Zähnezahl 17 ergibt sich aus der Bearbeitungsmethode und hängt auch von dieser ab. Wenn Sie die Bearbeitungsmethode für Zahnräder ändern oder verbessern, zum Beispiel durch eine Formungsmethode oder Verschiebungsbearbeitung (hier speziell auf geradzahnige Zylinderschneiden bezogen), tritt kein Unterfutterungsphänomen auf, und es gibt keine Begrenzung bei der Zähnezahl 17.

Außerdem lässt sich anhand dieser Frage und deren Antworten erkennen, dass eine charakteristische Eigenschaft des Maschinenbaus die enge Verbindung von Theorie und Praxis ist.

Meinung eines Internutzers: Erstens ist die Aussage, dass Zahnräder mit weniger als 17 Zähnen nicht rotieren können, falsch. Lassen Sie uns kurz erläutern, wie sich die Zahl 17 ergeben hat.

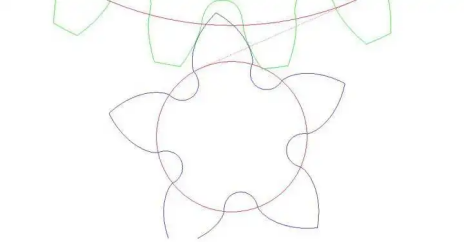
Zahnräder sind mechanische Bauteile mit Zähnen am Rand, die kontinuierlich ineinander greifen, um Bewegung und Kraft zu übertragen. Zahnradschneiderprofile umfassen unter anderem Evolventen- und Kreisbogenschneider, wobei Evolventenzahnräder weitgehend verbreitet sind.

Zylindergetriebe mit geraden Zähnen werden in gerade- und schrägverzahnte Zylindergetriebe unterteilt, usw. Bei normalem geradeverzahnten Zylindergetriebe beträgt der Koeffizient der Kopfhöhe 1, der Koeffizient der Fußhöhe 1,25 und der Druckwinkel 20°. Die Bearbeitung von Zahnradern verwendet im Allgemeinen die Erzeugungsmethode, das heißt, die Bewegung des Werkzeugs und des Zahnrads während der Bearbeitung ähnelt dem Eingriff eines Paars von Zahnrädern. Bei der Bearbeitung eines normalen Zahnrades wird, wenn die Zähnanzahl kleiner als ein bestimmter spezifischer Wert ist, die Evolventenkurve am Fuß des Zahnrads abgeschnitten, was als Unterfütterung bezeichnet wird, wie in der linken Abbildung unten gezeigt. Unterfütterung beeinflusst die Stärke des Zahnrads und die Glattheit der Übertragung erheblich. Der minimale Wert, bei dem keine Unterfütterung auftritt, beträgt 2*1/sin(20)^2 (1 ist der Koeffizient der Kopfhöhe, 20 ist der Druckwinkel).

Die Zähnezahl 17 gilt hier für normale geradzahnige Zylinderschneiden. Wir haben viele Möglichkeiten, das Unterschneiden zu vermeiden, wie zum Beispiel das Verstellen der Räder, das heißt, das Werkzeug von oder auf die Rotationsachse des Zahnbereichs zu bewegen. Um hier ein Unterschneiden zu vermeiden, muss man wählen, sich vom Konturmittelpunkt wegzubewegen, wie in der rechten Abbildung unten gezeigt, und das vollständige Evolventenprofil erscheint erneut.

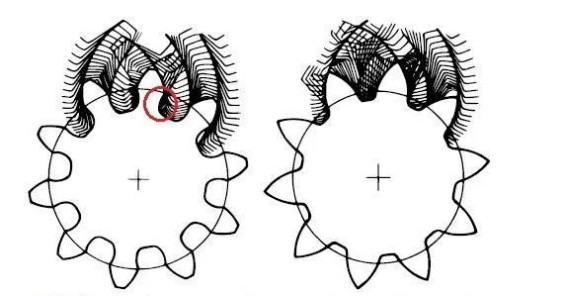
Nach dem Verstellen kann das Rad sich drehen, ohne beeinträchtigt zu werden. Wie oben gezeigt, kann durch geeignete Verschiebung auch ein Rad mit 5 Zähnen sich drehen. Tatsächlich können auch Schrägverzahnungen Unterschneiden vermeiden oder die minimale Zähnezahl verringern, bei der ein Unterschneiden auftritt.

T die Zahl 17 wird berechnet. Es ist nicht so, dass Räder mit weniger als 17 Zähnen nicht rotieren können, aber wenn es weniger als 17 Zähne gibt, ist es leicht, während der Zahnradsbearbeitung einen Teil der Involutkurve am Zahnboden abzuschneiden, was als Unterfütterung (undercutting) schwächt die Stärke des Zahnrads. Was die Berechnung betrifft, handelt es sich vollständig um ein mathematisches Problem, siehe oben genannte Formel, mit dem Verklappwinkel a=20 Grad, ist die minimale Zähnezahl ohne Unterfütterung 17.

Meinung eines Internutzers: Ob die Anzahl der Zahnradaugen unter 17 liegen kann, ist eine Frage, die berücksichtigt werden sollte. Bei Standardzahnrädern darf die Zähnezahl wirklich nicht unter 17 liegen. Warum? Weil es bei einer Zähnezahl unter 17 zu einem Unterfütterungsphänomen kommt.

Der sogenannte Unterfütterungseffekt bezieht sich auf den Zustand, bei dem die Zahnspitzenlinie des Werkzeugs unter bestimmten Bedingungen zu tief in das Zahnfußbereich der Getriebe schneidet, während der Generationsmethode zur Getriebefertigung angewendet wird, und ein Teil der Involutkurve am Zahnfuß abgeschnitten wird.

Generationsmethode

Die Generiermethode (auch als Entwicklungsverfahren bekannt) ist eine Zahnradbearbeitungstechnik, die das Umhüllprinzip aus der Geometrie nutzt. Nachdem die Evolventenzahnprofile und die Winkelgeschwindigkeit w1 des Antriebsrades gegeben sind, kann die Winkelgeschwindigkeit w2 des angerissenen Rades durch das Eingreifen der beiden Zahnräder ermittelt werden, und das Übersetzungsverhältnis i12 = w1/w2 ist ein konstanter Wert. Dies liegt daran, dass während des Eingriffs der beiden Zahnräder die beiden Teilkreise reine Rollbewegung ausführen. Während der Teilkreis 1 rein auf dem Teilkreis 2 rollt, nimmt das Zahnprofil von Rad 1 eine Reihe relativer Positionen bezüglich Rad 2 ein, und die Umhüllende dieser relativen Positionen ist das Zahnprofil von Rad 2. Anders ausgedrückt: Während der reinen Rollbewegung der beiden Teilkreise können die beiden Evolventenzahnprofile als Umhüllende voneinander betrachtet werden.

Unterschnitt-Phänomen

Die Ursache von Unterfütterung: Wenn der Schnittpunkt der Zahnspitzlinie des Werkzeugs mit der Verzahnungslinie den Verzahnungsgrenzpunkt N1 überschreitet und das Werkzeug weiter von Position Ⅱ bewegt, wird ein Teil des am Zahnfuß bereits gefertigten Evolventenprofils abgeschnitten.

Die Folgen der Unterfütterung: Ein Rad mit starkem Unterfütterungsschaden schwächt einerseits die Biegestärke der Zähne; andererseits verringert es den Grad der Getriebeübertragung, was sehr ungünstig für die Übertragung ist. Die Ursache von Unterfütterung: Wenn der Schnittpunkt der Zahnspitzlinie des Werkzeugs mit der Verzahnungslinie den Verzahnungsgrenzpunkt N1 überschreitet und das Werkzeug weiter von Position Ⅱ bewegt, wird ein Teil des am Zahnfuß bereits gefertigten Evolventenprofils abgeschnitten.

Bei nicht-standardisierten Rädern ist eine Anzahl von weniger als 17 Zähnen akzeptabel.

Nachdem all dies gesagt wurde, was ist deine Meinung? Fühle dich frei, einen Kommentar zu hinterlassen und ihn zu teilen~